ACCA F9/FM Lecture | Quản lý tiền với mô hình Miller-Orr & Baumol Model

Tiếp theo bài viết về Chính sách quản lý vốn lưu động & quản lý Hàng tồn kho, trong bài viết này Ad sẽ đi làm rõ các nội dung liên quan đến quản lý tiền trong doanh nghiệp (“Cash management”) với 2 mô hình Miller-Orr và Baumol Model.

1. Cash management là gì?

“Cash management” tạm dịch là Quản lý tiền. Quản lý tiền là 1 nội dung trong Quản lý Vốn lưu động (“Working capital Management”) của doanh nghiệp.

1 doanh nghiệp thông thường sẽ nắm giữ tiền với 3 động cơ:

• Thứ 1 là để đảm bảo tính thanh khoản hay tối thiểu rủi ro mất thanh khoản. Nghĩa là để đảm bảo đủ tiền cho các hoạt động kinh doanh hàng ngày (“Transactions motive”).
• Thứ 2 là để phòng ngừa các sự kiện đột biến phát sinh (“Precautionary motive”). Ví dụ, khi doanh thu của doanh nghiệp bị sụt giảm đột biến dẫn đến nguồn tiền vào bị suy giảm nghiêm trọng.
• Thứ 3 là để chờ khi cơ hội đầu tư tốt thì thực hiện (“Speculation motive”). Ví dụ, dự đoán thị trường bất động sản sẽ xuống đáy trong thời gian tới thì doanh nghiệp có thể sẽ muốn dự trữ tiền để mua được sản phẩm với giá tốt.

Tuy nhiên, việc nắm giữ tiền quá nhiều cũng giống như nắm giữ các loại tài sản khác: Sẽ phát sinh chi phí cơ hội. Đó chính là lợi nhuận bị mất đi khi công ty không sử dụng tiền để đầu tư, phát triển kinh doanh kiếm lời ở hiện tại.

Ngược lại, nếu mức thanh khoản quá thấp, hiểu là dự trữ ít tiền, thì sẽ gia tăng khả năng kiếm lời ở hiện tại cho doanh nghiệp. Nhưng lại dẫn đến rủi ro mất thanh khoản hoặc bị bỏ lỡ cơ hội đầu tư tốt khi chúng xuất hiện. Do vậy:

Cũng giống như Quản lý vốn lưu động nói chung, việc quản lý tiền là nhằm đảm bảo sự cân bằng giữa 2 mục tiêu có sự đánh đổi về bản chất này: Tính thanh khoản và Khả năng kiếm lợi nhuận. Hay nói cách khác là xác định mức dự trữ tối ưu giúp tối thiểu chi phí liên quan đến việc nắm giữ tiền.

Trong phạm vi môn F9/FM Financial Management chúng ta sẽ đi xem xét 2 mô hình cung cấp thông tin về vấn đề này: Baumol và Miller-Orr.

2. Mô hình Baumol là gì?

Nói một cách khái quát thì mô hình Baumol là mô hình xác định mức dự trữ tiền tối ưu, hay mức bổ sung tiền tối ưu bằng cách cân bằng giữa chi phí nắm giữ tiền và chi phí giao dịch, hay chi phí chuyển đổi từ chứng khoán sang tiền.

Nếu bạn nào đã tìm hiểu về mô hình quản lý hàng tồn kho EOQ sẽ thấy rằng, mô hình Baumol thực chất là sự áp dụng mô hình EOQ trong quản lý hàng tồn kho sang quản lý tiền. Sự khác biệt là, đối tượng hàng hoá của mô hình Baumol là “Tiền”.

Ad cũng nói thêm chút rằng, có nhiều tranh cãi về việc gọi tên của mô hình này. Lý do xuất phát từ tranh luận ai mới là người đầu tiên đưa ra luận điểm: William J. Baumol hay James Toubin? Câu trả lời chính xác thì Ad cũng không biết. Nhưng cho đến hiện tại, Baumol vẫn là tên được sử dụng phổ biến hơn. Sau đây chúng ta hãy cùng đi tìm hiểu về nguyên lý cơ bản của mô hình này nhé.

[1] Nguyên lý của mô hình Baumol

Để dễ hình dung, chúng ta hãy xem xét tình huống như sau:

Giả sử 1 doanh nghiệp có nhu cầu sử dụng tiền trong cả năm là D. Số tiền này sẽ được sử dụng ổn định trong cả năm. Doanh nghiệp này nắm giữ một lượng chứng khoán có thể dễ dàng bán ngay lập tức trên thị trường để thu tiền về khi cần.

Đầu năm, doanh nghiệp sẽ dự trữ số tiền là Q để tiêu dùng. Sau đó trong năm sẽ phát sinh các khoản chi làm số tiền này bị giảm đi về 0. Khi đó, công ty sẽ phải bổ sung thêm 1 lượng tiền là Q để đạt được mức dự trữ như đầu năm. Việc bổ sung tiền sẽ được thực hiện bằng cách bán đi 1 lượng chứng khoán của công ty để thu tiền về. Chu trình này được lặp đi lặp lại trong năm.

Ta có thể mô tả sự biến động của số dư tiền theo mô hình Baumol như sau:

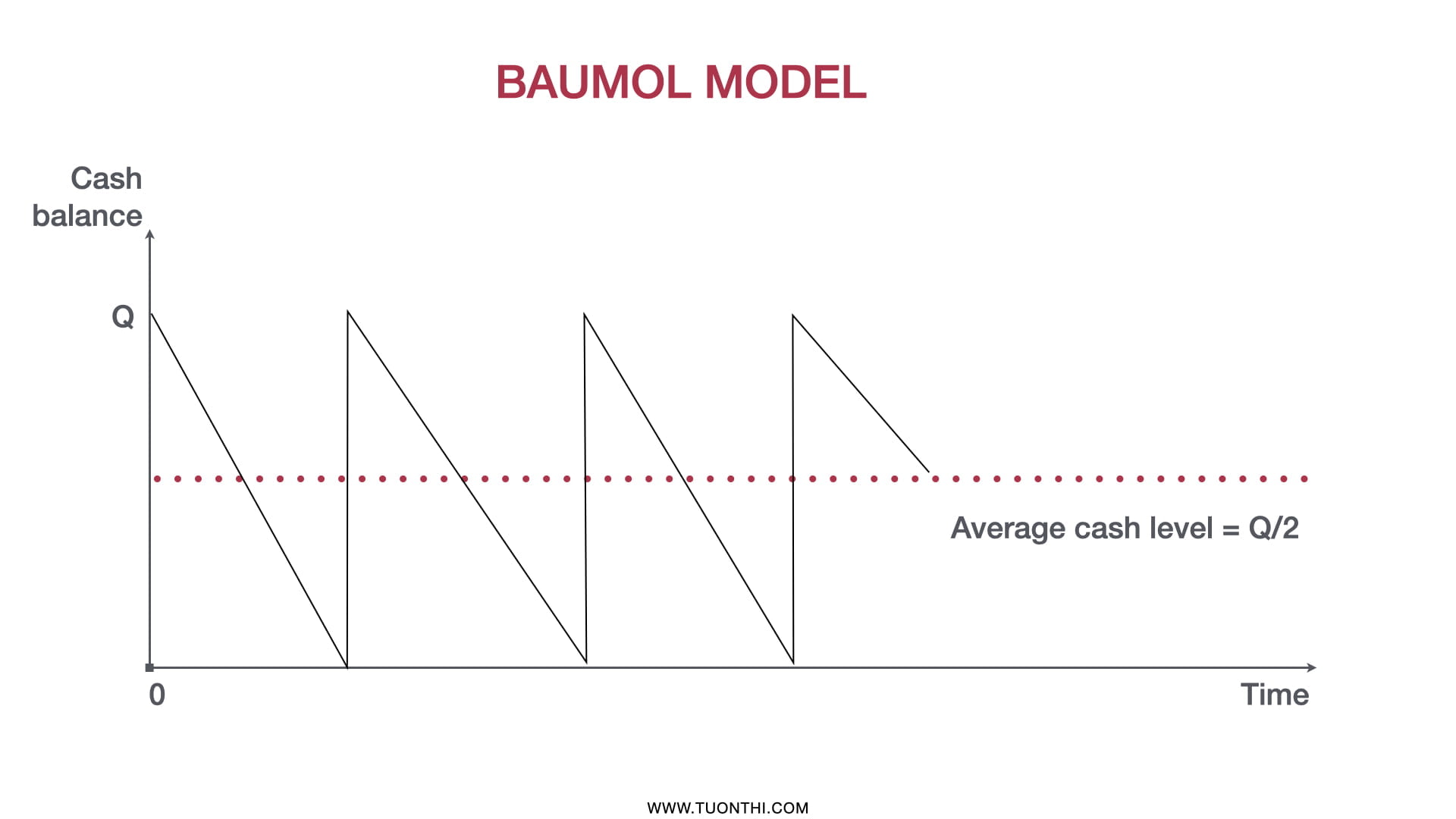
Biết rằng, chi phí để bán chứng khoán thu tiền về là C_o/giao dịch. Và khoản đầu tư vào chứng khoán mang lại cho công ty 1 khoản lợi nhuận ổn định là i%/năm.

Như vậy:

• Số dư tiền trung bình trong tháng là: Q/2
• Chi phí dự trữ tiền (“Holding cost”): i% * Q/2
• Số lượng giao dịch chuyển đổi từ chứng khoán sang tiền thực hiện trong năm: D/Q
• Chi phí giao dịch, chi phí đặt hàng hay chi phí chuyển đổi (“Transaction cost”): C_o *D/Q

Trong khi đó, chi phí dự trữ tiền thì biến động cùng chiều còn chi phí giao dịch thì biến động ngươc chiều với số tiền dự trữ hay số tiền quy đổi của mỗi giao dịch. Do vậy, mức dự trữ hay quy đổi tối ưu sẽ là mức mà tại đó cân bằng được giữa chi phí dự trữ tiền và chi phí giao dịch.

i% * Q / 2  =  C_o * D / Q

Biến đổi 2 vế của phương trình ta sẽ xác định được Q theo công thức:

Q = √(2*C_o*D / i )

Trong đó:

• Q: số tiền cần bổ sung của mỗi giao dịch chuyển đổi từ chứng khoán sang tiền
• C_o: chi phí để bán chứng khoán thu tiền về (Ordering cost hay Transaction cost) của 1 giao dịch
• D: số lượng tiền cần sử dụng trong kỳ
• i: chi phí cơ hội của việc nắm giữ tiền, thể hiện qua %lợi nhuận/kỳ mà doanh nghiệp bị bỏ lỡ. Lưu ý, nếu kỳ xem xét là năm/quý/tháng thì i sẽ là %lãi suất tương ứng lần lượt của năm/quý/tháng.

Thì đây chính là cách xác định số tiền dự trữ hay số tiền cần bổ sung tối ưu theo mô hình Baumol. Cùng đi xem 1 vài ví dụ để hiểu rõ hơn nhé.

[2] Ví dụ minh hoạ mô hình Baumol

Ví dụ 1. 1 công ty cần $150,000 mỗi năm cho các khoản thanh toán thường xuyên. Để chuyển đổi các khoản đầu tư ngắn hạn sang tiền sẽ làm công ty phát sinh chi phí cố định là $400/giao dịch. Các khoản đầu tư ngắn hạn này mang lại cho công ty khoản thu nhập tài chính là 5%/năm. Trong khi đó, nếu công ty mang tiền gửi tiết kiệm thì sẽ kiếm được khoản thu nhập là 1%/năm.

Yêu cầu: Xác định giá trị tối ưu của giao dịch chuyển đổi từ khoản đầu tư ngắn hạn sang tiền theo mô hình Baumol?

Trả lời:

Từ thông tin tình huống cung cấp, chúng ta xác định được các chỉ tiêu sau:

• D = $150,000
• i = 5%/năm – 1%/năm = 4%/năm
• C_o = $400

Do đó, giá trị tối ưu của mỗi giao dịch quy đổi sẽ là: Q = √(2*C_o*D / i ) = √(2*$400*$150,000 / 4%) = 54,772 

Ví dụ 2. 1 công ty cần $0.5m cho các khoản chi trong giai đoạn 5 tháng tới. Hiện tại công ty đang có các khoản chứng khoán niêm yết trị giá tương đương số tiền này. Biết rằng các chứng khoán này có thể mang lại tỷ suất lợi nhuận là 18%/năm. Việc chuyển đổi từ chứng khoán sang tiền mặt sẽ làm phát sinh chi phí cố định là $500/giao dịch.

Yêu cầu: Xác định giá trị tối ưu của giao dịch chuyển đổi từ chứng khoán sang tiền theo mô hình Baumol?

Trả lời:

Từ thông tin tình huống cung cấp, chúng ta xác định được các chỉ tiêu sau:

• D = $0.5m (kỳ 5 tháng)
• Chi phí cơ hội của việc nắm giữ tiền cho giai đoạn 5 tháng: i = 18% * 5/12 = 7.5%
• C_o = $500

Do đó, giá trị tối ưu của mỗi giao dịch quy đổi sẽ là: Q = √(2*C_o*D / i ) = √(2*$500*$0.5m / 7.5%) = $81,650

[3] Giả định của mô hình Baumol

Thông qua phần trên, chúng ta có thể thấy rằng mô hình Baumol được xây dựng dựa trên 1 số giả định sau:

• Tiền mặt được sử dụng ổn định theo thời gian.
• Doanh nghiệp dự đoán được chính xác nhu cầu sử dụng tiền trong kỳ
• Doanh nghiệp nắm giữ một lượng chứng khoán có thể dễ dàng bán ngay lập tức trên thị trường để thu tiền về khi cần
• Chi phí cơ hội của việc dự trữ tiền là có thể xác định được và không đổi theo thời gian
• Chi phí giao dịch (chuyển đổi từ chứng khoán sang tiền) là không đổi, bất kể quy mô giao dịch
• Chi phí liên quan đến việc nắm giữ tiền chỉ bao gồm 2 loại: chi phí cơ hội và chi phí giao dịch/chi phí chuyển đổi

Tuy nhiên những giả định này là không thực tế. Ví dụ, trong thực tế gần như không thể dự đoán 1 cách chắc chắn số tiền cần dùng trong kỳ. Hay lãi suất thường biến động nhiều dẫn đến chi phí cơ hội của việc nắm giữ tiền cũng sẽ biến động…

Do vậy, những giả định này lại trở thành nhược điểm của mô hình Baumol. Chưa kể đến là mô hình này còn không xem xét mức dự trữ tiền tối thiểu (Minimum/Buffer level). Trong khi đó, 1 doanh nghiệp sẽ không bao giờ để tình trạng số dư tiền về 0 rồi mới bổ sung thêm.

Để khắc phục nhược điểm này, các mô hình khác đã ra đời. Và mô hình Miller-Orr là một trong số đó.

3. Mô hình Miller-Orr là gì?

Khác với mô hình Baumol giả định dòng tiền của doanh nghiệp là chắc chắn, ổn định. Mô hình Miller-Orr giả định rằng:

Các dòng tiền ra/vào của doanh nghiệp là hoàn toàn không dự đoán được. Do vậy, doanh nghiệp chỉ có thể quản lý tiền theo phạm vi biến động của số dư tiền (“Spread”). Đây cũng chính là cơ sở xây dựng của mô hình Miller-Orr.

[1] Nguyên lý của mô hình Miller Orr là gì?

Mô hình Miller Orr có mục tiêu quản lý tiền sao cho số dư không vượt qua mức giới hạn cho phép. Ta có thể mô tả sự biến động của số dư tiền theo mô hình Miller-Orr như sau:

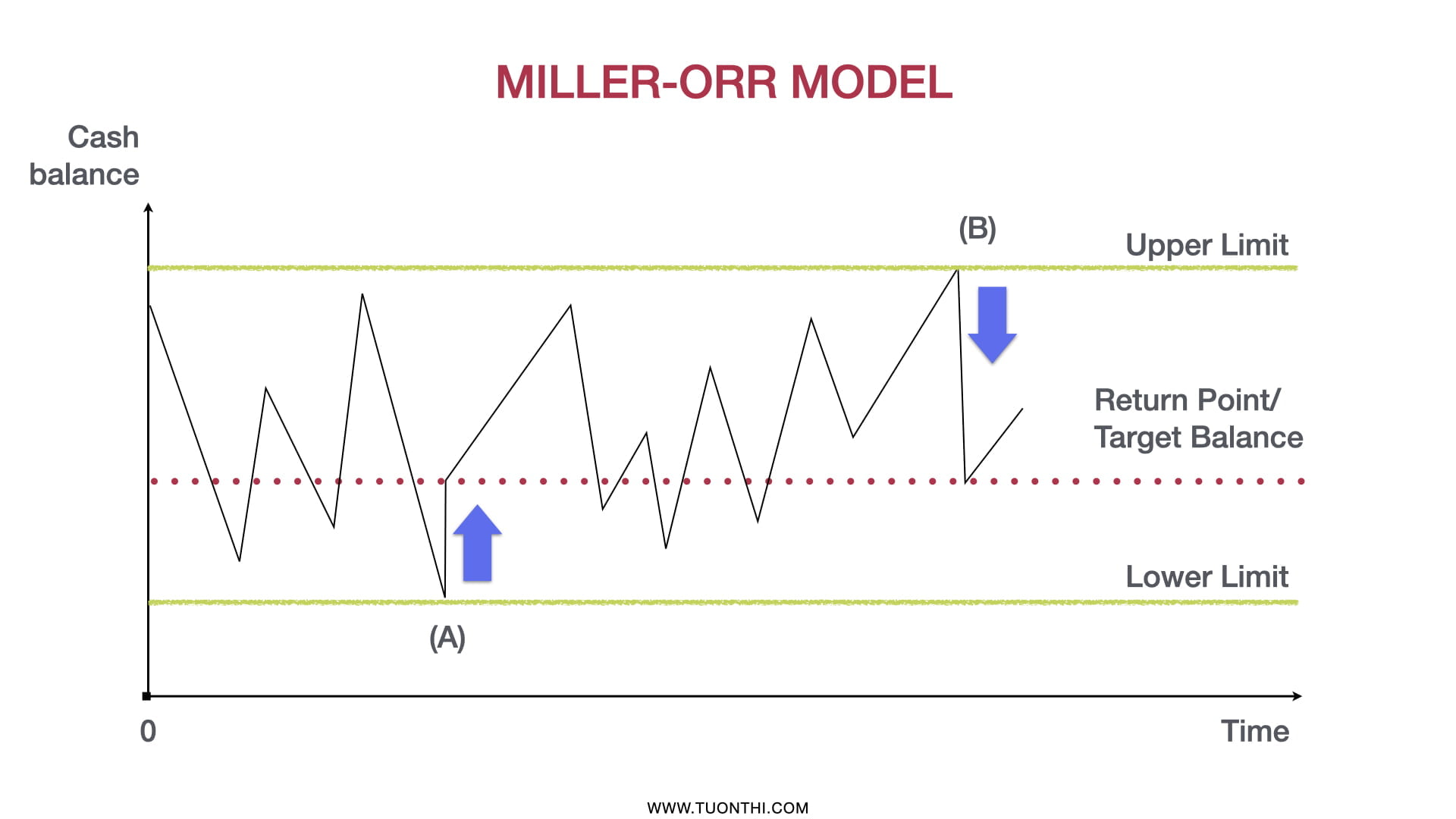
Nhìn vào hình ảnh này, ta có thể thấy rằng, theo mô hình Miller-Orr thì số dư tiền của doanh nghiệp sẽ biến động liên tục qua mỗi ngày. Tuy nhiên, luôn dao động trong phạm vi giữa Giới hạn trên (“Upper limit”) & Giới hạn dưới (“Lower limit”), và dao động xung quanh số dư tiền mục tiêu (“Return point”).

• Nếu số dư tiền chạm mức Giới hạn trên (“Upper limit”) – Điểm B trên đồ thị: Công ty sẽ sử dụng tiền để mua chứng khoán nhằm làm giảm số dư tiền về số dư mục tiêu (“Return point”).
• Nếu số dư tiền chạm mức Giới hạn dưới (“Lower limit”) – Điểm A trên đồ thị: Công ty sẽ bán chứng khoán thu tiền về để tăng số dư tiền về số dư mục tiêu (“Return point”).

Các chỉ tiêu vừa được đề cập trên đây sẽ được xác định như sau:

Giới hạn dưới (“Lower limit”): Mỗi công ty sẽ tự thiết lập một mức riêng.

Giới hạn trên (“Upper limit”) = Giới hạn dưới (“Lower limit”) + Phạm vi biến động của số dư tiền (“Spread”)

Còn số dư tiền mục tiêu (“Return point”) và phạm vi biến động của số dư tiền được xác định theo công thức:

Trong đó:

• “Transaction costs” – Chi phí giao dịch: Là chi phí phát sinh để mua bán chứng khoán / ngày
• “Variance of cash” – Biến động của số dư tiền / ngày

Cùng đi xem ví dụ sau để hiểu rõ hơn nhé.

[2] Ví dụ minh hoạ mô hình Miller-Orr

Ví dụ 3. Ban quản lý của S đã xây dưng số dư tiền mặt an toàn là $50,000. Độ lệch chuẩn (σ) của số dư tiền mặt hàng ngày trong năm qua là $37,500 và chi phí giao dịch là $75/ngày. Công ty cũng có cơ hội đầu tư tiền nhàn rỗi vào chứng khoán và có thể bán được với tỷ suất lợi nhuận hàng năm là 8%.

Yêu cầu: Tính toán các chỉ tiêu theo mô hình Miller-Orr?

Trả lời:

Từ thông tin trong tình huống, ta xác định được các chỉ tiêu sau:

• Daily Cash Variance = σ^{^2} = $37,500^{^2}
• Daily interest rate = 8%/365 ngày = 0.022%/ngày
• Daily transaction cost = $75/ngày
• Lower Limit = $50,000
• Spread = 3 * [3/4 * $75 * $37,500^{^2} / 0.022%]^{^1/3}= $213,325
• Upper Limit = Lower Limit + Spread = $50,000 + $213,325 = $263,325
• Return point = Lower Limit + 1/3 Spread = $50,000 + 1/3 * $213,325 = $121,108

[3] Giả định của mô hình Miller-Orr

Mô hình Miller-Orr được xây dựng dựa trên 1 số giả định sau:

• Dòng tiền vào và dòng tiền ra là ngẫu nhiên. Nói cách khác, mỗi ngày một doanh nghiệp có thể có cả các khoản thanh toán tiền mặt khác nhau và các khoản thu tiền mặt khác nhau.
• Số dư tiền mặt hàng ngày được phân phối bình thường, tức là xảy ra ngẫu nhiên.
• Công ty có khả năng đầu tư tiền nhàn rỗi vào chứng khoán
• Công ty có thể bán chứng khoán thu tiền về ngay lập tức khi cần, không có độ trễ về thời gian
• Tỷ lệ lợi nhuận hay chi phí giao dịch là không thay đổi

Cũng giống như mô hình Baumol, các giả định cũng chính là những hạn chế của mô hình Miller-Orr:

• Mô hình này giả định các yếu tố: chi phí giao dịch, tỷ suất lợi nhuận kiếm được hàng ngày là không đổi. Nhưng trong thực tế, những yếu tố này sẽ có thể thay đổi.
• Chỉ tiêu Biến động của số dư tiền (“Cash Variance”) mà mô hình này sử dụng, được xác định dựa trên thông tin trong quá khứ. Do vậy, có thể kết quả tính ra sẽ không phản ánh được hợp lý diễn biến trong tương lai, khi phát sinh sự thay đổi. Ví dụ nếu môi trường kinh tế hoặc cạnh tranh thay đổi làm ảnh hưởng đến hoạt động của công ty.
• Mô hình không xem xét tác động của yếu tố thời vụ trong hoạt động kinh doanh của doanh nghiệp. Trong khi đó, đối với một nhà bán lẻ, các yếu tố thời vụ có khả năng ảnh hưởng lớn đến dòng tiền vào.
• Mô hình giả định biến động tăng giảm trong ngày của số dư tiền sẽ không xác định trước được. Nghĩa là được phân phối hoàn toàn ngẫu nhiên trong ngày. Gỉa định này là không thực tế.

Uhm, như vậy là Ad đã giải thích tương đối về việc quản lý tiền cũng như 2 mô hình Baumol và Miller-Orr. Các bạn có thể tham khảo thêm Video bài giảng liên quan nhé.