Dạng bài này tương ứng Chương 3 trong đề cương ôn tập của VACPA. Và là 1 trong 3 dạng bài “thần thánh” tính đến thời điểm hiện tại.
Có thể bạn quan tâm: Tổng hợp các dạng bài tập Đề thi CPA môn Tài chính
Dạng bài này xoay quanh các yêu cầu
- Tính tỷ suất sinh lời kỳ vọng và độ lệch chuẩn của từng cổ phiếu hoặc Danh mục đầu tư
- So sánh mức độ rủi ro của từng cổ phiếu hoặc Danh mục đầu tư
- Xác định rủi ro thị trường của cổ phiếu hoặc Danh mục đầu tư
Điểm khó khăn nhất của dạng bài này là các công thức tính toán không quen thuộc, không dễ hiểu nên thường thì chúng ta đều cố gắng học vẹt chứ không hiểu bản chất.
Để học dạng bài tập này hiệu quả nhất, mình sẽ bắt đầu với các khái niệm cốt lõi, sau đó chúng ta sẽ xem cách vận dụng các khái niệm này để xử lý tình huống bài tập trong đề thi CPA như nào.
Phần 1. Các khái niệm cốt lõi cần biết
1. Tỷ suất sinh lời kỳ vọng
Tỷ suất sinh lời kỳ vọng hiểu nôm na là tỷ lệ lợi nhuận mong muốn thu được khi bỏ tiền ra đầu tư. Ví dụ: Bạn bỏ ra 10 đồng vốn đầu tư vào 1 doanh nghiệp. Bạn hy vọng thu được 3 đồng lợi nhuận. Thì tỷ suất sinh lời kỳ vọng của bạn là: 3/10 = 30%. Đây là đứng trên góc độ bạn là nhà đầu tư nhé. Nếu đứng ở góc độ doanh nghiệp cần huy động vốn: tỷ suất sinh lời kỳ vọng của nhà đầu tư này sẽ chính là chi phí vốn của doanh nghiệp.
Dạng bài này sẽ chỉ đề cập đến khái niệm tỷ suất sinh lời kỳ vọng từ góc độ nhà đầu tư.
(i) Tỷ suất sinh lời kỳ vọng của cổ phiếu: là Tỷ suất sinh lời kỳ vọng trung bình của cổ phiếu trên các điều kiện thị trường khác nhau.

Trong đó: ri là lợi suất ở phương án i và pi là xác suất xảy ra của phương án i
(ii) Tỷ suất sinh lợi kỳ vọng trung bình của danh mục đầu tư: chính là tỷ suất sinh lợi kỳ vọng trung bình của các cổ phiếu trong danh mục.
Công thức tính: r(A) * %A trong danh mục + r(B) * %B trong danh mục + r(C) * %C trong danh mục
Ứng dụng: Tỷ suất sinh lời kỳ vọng là đầu vào của nhiều công thức tính toán khác. Và có thể sử dụng để xác định xem có nên thực hiện 1 khoản đầu tư hay không?
- Nếu Tỷ suất sinh lời kỳ vọng của nhà đầu tư > Tỷ suất sinh lợi đòi hỏi của khoản đầu tư => Lợi nhuận kỳ vọng mang lại bù đắp được rủi ro => Nên đầu tư
- Nếu Tỷ suất sinh lời kỳ vọng của nhà đầu tư < Tỷ suất sinh lợi đòi hỏi của khoản đầu tư => Lợi nhuận kỳ vọng mang lại không đủ để bù đắp rủi ro => Không nên đầu tư
2. Rủi ro
Là khả năng mà tỷ suất sinh lợi thực tế không đạt như tỷ suất sinh lời kỳ vọng của nhà đầu tư. Thông thường, rủi ro sẽ được chia làm 2 loại:
- Rủi ro thị trường (Rủi ro hệ thống): là rủi ro cố hữu của việc đầu tư. Đầu tư đi liền với rủi ro mà. Dù lựa chọn đầu tư vào đâu thì rủi ro này vẫn tồn tại. Rủi ro này được đo lường bằng hệ số beta (β) của khoản đầu tư so với thị trường.
- Rủi ro riêng biệt (Rủi ro phi hệ thống): là rủi ro gắn liền với từng khoản đầu tư mà bạn chọn. Do đó, rủi ro này có thể được giảm thiểu bằng cách đa dạng hóa danh mục đầu tư. Rủi ro riêng biệt được đo lường bằng Độ lệch chuẩn σ (Standard Deviation) của khoản đầu tư.
Ví dụ:
– Nếu bạn chỉ nắm giữ một cổ phiếu ngân hàng, tin xấu ngành ngân hàng sẽ ảnh hưởng mạnh đến lợi nhuận cổ phiếu của bạn (rủi ro phi hệ thống).
– Nếu khủng hoảng tài chính toàn cầu xảy ra, tất cả cổ phiếu đều giảm (rủi ro hệ thống).
Sở dĩ phải phân chia ra làm 2 loại vì bản chất khác nhau dẫn đến cách tính khác nhau. Như đã nói bên trên, Rủi ro thị trường đo lường bằng hệ số Beta trong khi rủi ro riêng biệt đo lường bằng Độ lệch chuẩn σ.
(*) Hệ số Beta (β): là thước đo cho biết mức độ nhạy của tỷ suất sinh lời kỳ vọng của một tài sản (ví dụ: cổ phiếu) so với lợi suất của thị trường chung.
Ý nghĩa
- β = 1 => Tài sản có mức rủi ro hệ thống bằng thị trường
- β > 1 => Tài sản có độ biến động cao hơn thị trường → rủi ro hơn
- β < 1 => Tài sản có độ biến động thấp hơn thị trường → rủi ro thấp hơn
(**) Tác động của rủi ro tới Tỷ suất sinh lời
Tỷ suất sinh lời mà nhà đầu tư đòi hỏi là tỷ suất sinh lời cần thiết tối thiểu phải đạt được khi thực hiện đầu tư sao cho có thể bù đắp được rủi ro đầu tư.
Tỷ suất sinh lời đòi hỏi= Lãi suất thực + Tỷ lệ lạm phát + Mức bù rủi ro = Lãi suất phi rủi ro + Mức bù rủi ro
Để ước tính Tỷ suất sinh lời đòi hỏi, chúng ta sẽ sử dụng mô hình CAPM: Re = Rf + ß (Rm – Rf)
Trong đó:
- Hệ số bê-ta: Hệ số rủi ro thị trường của khoản đầu tư
- Rf : Tỷ suất sinh lời đòi hỏi trong điều kiện không có rủi ro, ví dụ như lãi suất trái phiếu chính phủ
- Rm: Tỷ suất sinh lợi đòi hỏi của thị trường (tỷ suất sinh lời trung bình)
3. Phương sai & Độ lệch chuẩn
Phương sai Var (Variance): là giá trị trung bình tính theo phương pháp bình quân gia quyền của các bình phương chênh lệch giữa giá trị thực tế so với giá trị kỳ vọng. Hiểu đơn giản thì phương sai này đo lường sự chênh lệch giữa thực tế và kỳ vọng, hay nói cách khác là đo lường rủi ro.
Độ lệch chuẩn σ (Standard Deviation): Là mức độ sai lệch giữa tỷ suất sinh lời kỳ vọng và thực tế. Độ lệch chuẩn càng lớn thì mức độ sai lệch giữa tỷ suất sinh lời thực tế so với kỳ vọng càng lớn => Rủi ro không đạt kỳ vọng càng lớn => Như vậy, chúng ta cần tính ra Độ lệch chuẩn của từng khoản đầu tư để làm căn cứ so sánh rủi ro.
(i) Độ lệch chuẩn của cổ phiếu: là độ lệch giữa tỷ suất sinh lời kỳ vọng trung bình với tỷ suất sinh lời kỳ vọng riêng tương ứng với từng điều kiện thị trường:
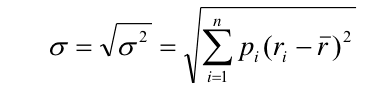
(ii) Độ lệch chuẩn của danh mục đầu tư:

Trong công thức này sẽ có 1 khái niệm mới là: Hiệp phương sai của danh mục Cov (i,j). Hiểu đơn giản là mối quan hệ rủi ro giữa hai cổ phiếu trong cùng một danh mục đầu tư nhé. Chi tiết các bạn xem ở mục 5 bên dưới.
4. Hệ số biến thiên (Coefficient of Variation – Cv)
Hệ số biến thiên Cv (Coefficient of Variation) đo lường rủi ro trên mỗi đơn vị lợi suất kỳ vọng
Công thức: Cv = Độ lệch chuẩn của tỷ suất sinh lời kỳ vọng (σ) / Tỷ suất sinh lời kỳ vọng (r)
Ý nghĩa:
- Cv giúp so sánh rủi ro của các khoản đầu tư có lợi suất kỳ vọng khác nhau. Cv càng thấp → Khoản đầu tư càng hiệu quả → nhà đầu tư chịu ít rủi ro hơn cho cùng một đơn vị lợi nhuận. Và ngược lại, Cv càng cao → Khoản đầu tư ít hiệu quả hơn → nhà đầu tư chịu nhiều rủi ro hơn cho cùng một đơn vị lợi nhuận.
- Từ góc độ danh mục đầu tư: Cv giúp đánh giá xem rủi ro của danh mục sẽ tăng lên hay giảm đi khi đầu tư vào 1 cổ phiếu cụ thể. Nếu Cv của cổ phiếu nào < Cv của danh mục thì nghĩa là đầu tư riêng vào cổ phiếu đó sẽ làm giảm rủi ro của danh mục và ngược lại.
5. Hiệp phương sai (Covariance – Cov) & Hệ số tương quan (Pairwise Correlation – ρ)
2 chỉ tiêu này đều phản ánh tương quan (mức độ thay đổi rủi ro) giữa hai khoản đầu tư bất kỳ trong danh mục đầu tư:
(i) Hiệp phương sai (Covariance – COV): Chỉ tiêu này đo lường mức độ thay đổi cùng nhau của hai hai khoản đầu tư bất kỳ trong danh mục đầu tư.
Hiệp phương sai của tỷ suất sinh lời của hai khoản đầu tư A,B:
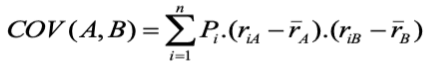
Trong đó:
- Pi: Xác suất xảy ra tình huống
- riA: Tỷ suất sinh lời của khoản đầu tư A ở tình huống i
- riB : Tỷ suất sinh lời của khoản đầu tư B ở tình huống i
- rA, rB: Tỷ suất sinh lời kỳ vọng của hai khoản đầu tư A và B
Ý nghĩa:
- COV (A,B) > 0: Tỷ suất sinh lợi của 2 khoản đầu tư có xu hướng biến động cùng chiều
- COV (A,B) < 0:Tỷ suất sinh lợi của 2 khoản đầu tư có xu hướng biến động ngược chiều
- COV (A,B) = 0: Không có mối quan hệ tuyến tính giữa 2 khoản đầu tư
Hiệp phương sai COV có đơn vị là bình phương lợi suất (ví dụ: %²), nên khó so sánh trực tiếp giữa các cặp tài sản => Sử dụng Hệ số tương quan dưới đây.
(ii) Hệ số tương quan (Pairwise Correlation – ρ): Hệ số tương quan là phiên bản chuẩn hóa của hiệp phương sai – nó cho biết mức độ và chiều hướng của mối quan hệ tuyến tính giữa hai biến, nằm trong khoảng từ -1 ~ 1. Vì không có đơn vị nên dễ sử dụng để so sánh, phổ biến hơn trong thực hành
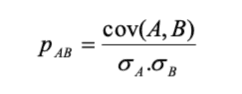
Ý nghĩa
- ρ = 1: 2 khoản đầu tư luôn biến động cùng chiều
- ρ = −1: 2 khoản đầu tư luôn biến đổi ngược chiều
- ρ = 0: không có mối quan hệ tuyến tính
Ví dụ: Hai cổ phiếu cùng ngành thường có ρ cao (≈ 0.6–0.9)
(*) Tổng kết ứng dụng của các khái niệm vào trong so sánh, đánh giá, lựa chọn khoản đầu tư hoặc danh mục đầu tư:
– Khi so sánh 2 khoản đầu tư riêng biệt:
- Nếu hai khoản đầu tư có cùng Tỷ suất sinh lời kỳ vọng (r): khoản đầu tư nào có độ lệch chuẩn σ càng cao thì mức rủi ro càng lớn.
- Nếu hai khoản đầu tư có Tỷ suất sinh lời kỳ vọng (r) khác nhau: Sử dụng hệ số biến thiên Cv để đánh giá. Khoản đầu tư nào có Cv lớn hơn thì rủi ro lớn hơn.
– Khi so sánh 2 Danh mục đầu tư: Danh mục đầu tư nào có Hệ số biến thiên Cv lớn hơn thì rủi ro lớn hơn.
Giờ chúng ta sẽ bắt đầu xử lý từng tình huống cụ thể trong đề thi nhé.
Phần 2. Bài tập minh hoạ trong đề thi CPA các năm
1. Đề thi CPA 2024 – Đề Chẵn
Yêu cầu 1. Bạn thu thập thông tin về tỷ suất sinh lợi hàng của cổ phiếu XYZ trong bảng dưới đây:
| 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| 8,5% | 9,2% | 12,0% | 11,0% | 13,0% | -2,0% | -16,0% | 2,0% | 10,5% | 13,0% |
Yêu cầu:
a. Hãy tính tỷ suất sinh lợi trung bình, phương sai, và độ lệch chuẩn của tỷ suất sinh lợi của cổ phiếu XYZ trong giai đoạn 2014-2023. (Sử dụng tỷ suất sinh lời trung bình cộng).
b. Giả sử lãi suất phi rủi ro là 3% và phần bù rủi ro thị trường (Rm-Rf) là 5%, theo bạn hệ số beta (β) của cổ phiếu XYZ sẽ trong khoảng bao nhiêu?
Đáp án
a. Lập bảng tính các chỉ tiêu yêu cầu
| Năm | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Tỷ suất sinh lợi kỳ vọng hàng năm (ri) | 8.50% | 9.20% | 12% | 11% | 13% | -2% | -16% | 2% | 10.50% | 13% |
| Tỷ suất sinh lợi kỳ vọng trung bình (Re) | 6.12% | |||||||||
| (ri – Re)^2 | 0.00057 | 0.00095 | 0.00346 | 0.00238 | 0.00473 | 0.006593 | 0.04893 | 0.00170 | 0.00192 | 0.00473 |
| Phương sai | 0.00760 | |||||||||
| Độ lệch chuẩn | 8.72% |
b. Tính hệ số bê-ta
Áp dụng công thức CAPM: Re = Rf + ßi (Rm – Rf)
Trong đó:
- Re: Tỷ suất sinh lợi kỳ vọng của tài sản (Re = 6.12%)
- Rf: Tỷ suất sinh lợi khi đầu tư vào tài sản phi rủi ro (Rf = 3%)
- Rm – Rf: Phần bù của thị trường khi đầu tư vào tài sản khác với tài sản phi rủi ro (Rm – Rf = 5%)
Thay số liệu vào công thức ta có giá trị Beta = 0.624
Ta thấy beta < 1 => Cổ phiếu có độ biến động thấp hơn thị trường → rủi ro thấp hơn
Yêu cầu 2. Bạn đầu tư vào 2 cổ phiếu A và B với các thông tin như trong bảng dưới đây:
| Chỉ tiêu | Cổ phiếu A | Cổ phiếu B |
|---|---|---|
| Tỷ suất sinh lời trung bình | 5%/năm | 20%/năm |
| Độ lệch chuẩn | 42%/năm | 55%/năm |
| Tỷ trọng đầu tư | 25% | 75% |
Yêu cầu:
a. Hãy tính tỷ suất sinh lời trung bình của danh mục.
b. Nếu hệ số tương quan giữa cổ phiếu A và cổ phiếu B là -0,3, phương sai của danh mục và độ lệch chuẩn của danh sẽ là bao nhiêu?
c. Đây có phải là sự kết hợp giúp giảm rủi ro không? Trả lời vắn tắt tại sao?
Đáp án
a và b. Tính các chỉ tiêu tỷ suất sinh lợi trung bình, phương sai và độ lệch chuẩn của danh mục
| Chỉ tiêu | Danh mục | ||
| A | B | ||
| Độ lệch chuẩn của tỷ suất sinh lời của cổ phiếu | 42% | 55% | |
| Tỷ trọng cổ phiếu | 25% | 75% | |
| Tỷ suất sinh lời trung bình kỳ vọng của cổ phiếu | 5.0% | 20.0% | |
| Tỷ suất sinh lời kỳ vọng của danh mục | 16.25% | ||
| Hiệp phương sai Cov(X,Y) với Hệ số tương quan P = – 0.3 | (0.07) | ||
| Phương sai của tỷ suất sinh lời của danh mục | 0.1552 | ||
| Độ lệch chuẩn của danh mục | 39.39% | ||
c. Đây có phải là sự kết hợp giúp giảm rủi ro không? Trả lời vắn tắt tại sao?
Vì 2 cổ phiếu có Hệ số tương quan P(X,Y) = – 0.3 < 0 => Hai cổ phiếu có mối quan hệ biến động ngược chiều trên thị trường => Sự kết hợp này sẽ giúp giảm rủi ro
2. Đề thi CPA 2024 – Đề Lẻ
Yêu cầu 1. Bạn thu thập thông tin về tỷ suất sinh lợi hàng năm của cổ phiếu ABC trong bảng dưới đây:
| 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| 11,0% | 12,5% | 8,0% | 9,0% | 13,0% | 7,0% | 15,0% | 2,0% | -16,5% | 11,0% |
Yêu cầu:
a. Hãy tính tỷ suất sinh lợi trung bình, phương sai, và độ lệch chuẩn của tỷ suất sinh lợi của cổ phiếu ABC trong giai đoạn 2014-2023. (Sử dụng tỷ suất sinh lời trung bình cộng).
b. Giả sử lãi suất phi rủi ro là 3,5% và phần bổ rủi ro thị trường (Rm-Rf) là 4,5%, theo bạn hệ số beta (β) của cổ phiếu ABC sẽ trong khoảng bao nhiêu?
Đáp án
a. Lập bảng tính các chỉ tiêu yêu cầu
Lưu ý: Tình huống này có sự biến đổi một chút so với thông thường. Thay vì đề bài đưa ra tỷ suất sinh lợi kỳ vọng của từng điều kiện thị trường thì bây giờ chúng ta sẽ có tỷ suất sinh lợi theo từng năm. Như vậy, công thức của chúng ta cũng sẽ biến đổi. Thay vì tính tỷ suất sinh lợi kỳ vọng dựa vào xác suất xảy ra thì chúng ta sẽ tính theo phương pháp đề bài yêu cầu là trung bình cộng. Tức là tính chia đều thôi, càng đơn giản.
| Năm | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Tỷ suất sinh lợi kỳ vọng hàng năm (r) | 11% | 12.50% | 8% | 9% | 13% | 7% | 15% | 2% | -16.50% | 11% |
| Tỷ suất sinh lợi kỳ vọng trung bình (Re) | 7.20% | |||||||||
| (r – Re)^2 | 0.00144 | 0.00281 | 0.00006 | 0.00032 | 0.00336 | 0.000004 | 0.00608 | 0.00270 | 0.05617 | 0.00144 |
| Phương sai | 0.00744 | |||||||||
| Độ lệch chuẩn | 8.63% |
b. Tính hệ số bê-ta
Áp dụng công thức CAPM: Re = Rf + ßi (Rm – Rf)
Trong đó:
- Re: Tỷ suất sinh lợi kỳ vọng của tài sản (Re = 7.2%)
- Rf: Tỷ suất sinh lợi khi đầu tư vào tài sản phi rủi ro (Rf = 3.5%)
- Rm – Rf: Phần bù của thị trường khi đầu tư vào tài sản khác với tài sản phi rủi ro (Rm – Rf = 4.5%)
Thay số liệu vào công thức ta có giá trị Beta = 0.822
Ta thấy beta < 1 => Cổ phiếu có độ biến động thấp hơn thị trường → rủi ro thấp hơn
Yêu cầu 2. Bạn đầu tư vào 2 cổ phiếu X và Y với các thông tin như trong bảng dưới đây:
| Chỉ tiêu | Cổ phiếu X | Cổ phiếu Y |
|---|---|---|
| Tỷ suất sinh lời trung bình | 8%/năm | 15%/năm |
| Độ lệch chuẩn | 45%/năm | 67%/năm |
| Tỷ trọng đầu tư | 35% | 65% |
Yêu cầu:
a. Hãy tính tỷ suất sinh lời trung bình của danh mục.
b. Nếu hệ số tương quan giữa cổ phiếu X và cổ phiếu Y là 0,3, phương sai của danh mục và độ lệch chuẩn của danh mục sẽ là bao nhiêu?
c. Đây có phải là sự kết hợp giúp giảm rủi ro không? Trả lời vắn tắt tại sao?
Đáp án
a và b. Tính các chỉ tiêu tỷ suất sinh lợi trung bình, phương sai và độ lệch chuẩn của danh mục
| Chỉ tiêu | Danh mục | ||
| X | Y | ||
| Độ lệch chuẩn của tỷ suất sinh lời của cổ phiếu | 45% | 67% | |
| Tỷ trọng cổ phiếu | 35% | 65% | |
| Tỷ suất sinh lời kỳ vọng của cổ phiếu | 8.0% | 15.0% | |
| Tỷ suất sinh lời kỳ vọng của danh mục | 12.55% | ||
| Hiệp phương sai Cov(X,Y) với Hệ số tương quan P = 0.3 | 0.09 | ||
| Phương sai của tỷ suất sinh lời của danh mục | 0.2556 | ||
| Độ lệch chuẩn của danh mục | 50.56% | ||
c. Đây có phải là sự kết hợp giúp giảm rủi ro không? Trả lời vắn tắt tại sao?
Vì 2 cổ phiếu có Hệ số tương quan P(X,Y) = 0.3 < 1 => Hai cổ phiếu có mối quan hệ biến động cùng chiều trên thị trường => Sự kết hợp này sẽ không giúp giảm rủi ro
3. Đề thi CPA 2022 – Đề Chẵn
Tình huống. Cho thông tin về dự báo tình trạng kinh tế và tỷ suất sinh lợi dự báo cho từng cổ phiếu như bảng dưới đây. Lưu ý, cổ phiếu Z là cổ phiếu thuộc nhóm ngành phòng thủ nên được dự báo có thành quả tốt hơn trong điều kiện kinh tế không thuận lợi.
| Tình trạng kinh tế | Xác suất | Cổ phiếu X | Cổ phiếu Y | Cổ phiếu Z |
|---|---|---|---|---|
| Suy thoái | 10,0% | -5,0% | 5,0% | 10,0% |
| Ổn định | 70,0% | 11,0% | 9,0% | 6,0% |
| Tăng trưởng | 20,0% | 25,0% | 11,0% | 5,0% |
Yêu cầu
a. Tính tỷ suất sinh lợi kỳ vọng của từng cổ phiếu.
b. Tính độ lệch chuẩn của từng cổ phiếu.
c. Nếu nhà đầu tư muốn xây dựng danh mục đầu tư P gồm 2 cổ phiếu với tỷ trọng bằng nhau, thì nên chọn cặp cổ phiếu XY, XZ hay YZ để kết hợp với nhau nhằm đem lại độ lệch chuẩn thấp nhất cho danh mục? Giải thích.
d. Tính tỷ suất sinh lợi kỳ vọng và độ lệch chuẩn của danh mục P.
Bài giải
Lập bảng tính chi tiết để làm cơ sở thực hiện các yêu cầu của đề bài:
| Trạng thái nền kinh tế | Xác suất Pi | Cổ phiếu X | Cổ phiếu Y | Cổ phiếu Z | |||||||||
| Tỷ suất sinh lời ri | Pi * ri | pi * (ri – r)^2 | ri-rX | Tỷ suất sinh lời ri | Pi * ri | pi * (ri – r)^2 | ri-rY | Tỷ suất sinh lời ri | Pi * ri | pi * (ri – r)^2 | ri-rz | ||
| Suy thoái | 10% | -5% | -0.005 | 0.0029584 | -17.20% | 5% | 0.005 | 0.000160 | -4.00% | 10% | 1.00% | 0.000144 | 3.80% |
| Bình thường | 70% | 11% | 0.077 | 0.0001008 | -1.20% | 9% | 0.063 | 0.000000 | 0.00% | 6% | 4.20% | 0.000003 | -0.20% |
| Bùng nổ | 20% | 25% | 0.05 | 0.0032768 | 12.80% | 11% | 0.022 | 0.000080 | 2.00% | 5% | 1.00% | 0.000029 | -1.20% |
| 12.20% | 0.634% | 9.00% | 0.024% | 6.20% | 0.018% | ||||||||
YCa & b. Tính tỷ suất sinh lời kỳ vọng và độ lệch chuẩn cho từng cổ phiếu
| Kết quả % | Cổ phiếu X | Cổ phiếu Y | Cổ phiếu Z |
| Tỷ suất sinh lời kỳ vọng | 12.2% | 9.0% | 6.2% |
| Phương sai | 0.634% | 0.024% | 0.018% |
| Độ lệch chuẩn | 7.960% | 1.549% | 1.327% |
YC c &d. Xác định danh mục đầu tư 2 cổ phiếu để mang lại độ lệch chuẩn thấp nhất
Có 3 cổ phiếu nên chúng ta sẽ có 3 danh mục cần xem xét.
| Chỉ tiêu | Danh mục 1 | Danh mục 2 | Danh mục 3 | ||||
| X | Y | X | Z | Y | Z | ||
| Tỷ trọng cổ phiếu | 50% | 50% | 50% | 50% | 50% | 50% | |
| Tỷ suất sinh lời kỳ vọng của cổ phiếu | 12.20% | 9.00% | 12.20% | 6.20% | 9.00% | 6.20% | |
| Tỷ suất sinh lời kỳ vọng của danh mục | 10.600% | 9.200% | 7.600% | ||||
| Hiệp phương sai Cov = P*(ri – rX) * (ri – rY) | 0.001200 | (0.000944) | (0.000200) | ||||
| Phương sai của danh mục | 0.002244 | 0.001156 | 0.000004 | ||||
| Độ lệch chuẩn của danh mục | 4.74% | 3.40% | 0.20% | ||||
Kết luận: Danh mục 2 cổ phiếu Y và Z sẽ có độ lệch chuẩn thấp nhất
4. Đề thi CPA 2022 – Đề Lẻ
Tình huống: Cho thông tin về hai cổ phiếu A và B như sau:
| Tình trạng nền kinh tế | Xác suất | Tỷ suất sinh lời Cổ phiếu A | Tỷ suất sinh lời Cổ phiếu B |
|---|---|---|---|
| Suy thoái | 0,2 | 0,06 | -0,2 |
| Bình thường | 0,55 | 0,07 | 0,13 |
| Bùng nổ | 0,25 | 0,15 | 0,33 |
Yêu cầu
a. Tính tỷ suất sinh lời kỳ vọng cho từng cổ phiếu.
b. Độ lệch chuẩn của từng cổ phiếu là bao nhiêu?
c. Nếu nhà đầu tư e ngại rủi ro thì nên đầu tư vào cổ phiếu nào? Tại sao?
d. Một nhà đầu tư muốn thiết lập danh mục đầu tư P gồm 2 cổ phiếu trên với tỷ trọng đầu tư vào A là 65%. Hãy tính tỷ suất sinh lời kỳ vọng và độ lệch chuẩn của danh mục P.
e. Nếu nhà đầu tư đặt mục tiêu tỷ suất sinh lời kỳ vọng của danh mục gồm 2 chứng khoán A và B ở mức 10,50% thì nên phân bổ vốn đầu tư như thế nào?
Bài giải
Lập bảng tính chi tiết để làm cơ sở thực hiện các yêu cầu của đề bài:
| Trạng thái nền kinh tế | Xác suất | Cổ phiếu A | Cổ phiếu B | Cov (A,B) = P*(ri – rA) * (ri – rB) | ||||||
| Tỷ suất sinh lời ri | Pi * ri | pi * (ri – r)^2 | ri-rA | Tỷ suất sinh lời ri | Pi * ri | pi * (ri – r)^2 | ri-rB | |||
| Suy thoái | 0.2 | 0.06 | 0.012 | 0.0001568 | -2.80% | -0.2 | -0.04 | 0.019719 | -31.40% | 0.00176 |
| Bình thường | 0.55 | 0.07 | 0.0385 | 0.0001782 | -1.80% | 0.13 | 0.0715 | 0.000141 | 1.60% | (0.00016) |
| Bùng nổ | 0.25 | 0.15 | 0.0375 | 0.000961 | 6.20% | 0.33 | 0.0825 | 0.011664 | 21.60% | 0.00335 |
| 8.80% | 0.13% | 11.40% | 3.15% | 0.00495 | ||||||
YC1 & 2. Tính tỷ suất sinh lời kỳ vọng và độ lệch chuẩn cho từng cổ phiếu
| Kết quả | Cổ phiếu A | Cổ phiếu B |
| Tỷ suất sinh lời kỳ vọng | 8.80% | 11.40% |
| Phương sai | 0.13% | 3.15% |
| Độ lệch chuẩn | 3.60% | 17.75% |
YC3. Nếu nhà đầu tư e ngại rủi ro thì nên đầu tư vào cổ phiếu nào?
Dựa theo nguyên tắc so sánh rủi ro của 2 khoản đầu tư, trong tình huống của chúng ta:
Cổ phiếu A có Cv = 3.6%/8.8% = 0.41
Cổ phiếu B có Cv = 17.75% / 11.4% = 1.56
Như vậy, cổ phiếu B có rủi ro lớn hơn. Nên nếu nhà đầu tư e ngại rủi ro thì nên đầu tư vào cổ phiếu A
YC4. Tỷ suất sinh lời kỳ vọng & độ lệch chuẩn của danh mục 2 cổ phiếu
| Chỉ tiêu | Cổ phiếu A | Cổ phiếu B |
| Tỷ trọng | 65.0% | 35% |
| Tỷ suất sinh lời kỳ vọng | 8.80% | 11.40% |
| Tỷ suất sinh lời kỳ vọng của danh mục | 9.71% | |
| Hiệp phương sai của danh mục Cov (A,B) | 0.004948 | |
| Phương sai của danh mục | 0.0066606 | |
| Độ lệch chuẩn của danh mục | 8.16% |
YC5. Nên phân bổ vốn đầu tư cho danh mục như thế nào khi tỷ suất sinh lời kỳ vọng vào danh mục của nhà đầu tư là 10.5%?
Gọi A là tỷ trọng cổ phiếu A trong danh mục => Tỷ trọng cổ phiếu B: 1 – A%
Ta có phương trình: 8.8% * A% + 11.4% * (1-A%) = 10.5%
Gỉai phương trình: A = 0.3462 hay 34.62%
Có thể bạn quan tâm: Bài giảng về Rủi ro và Tỷ suất sinh lời

Ad ơi, sửa công thức CV ở trên, bị ngược rồi kìa
Hi ad, ở đề lẻ 2011, câu 3 có cho dữ kiện hệ số tương quan của danh mục đầu tư A là 0,996; của danh mục đầu tư B là 0,999.Mình ko rõ sử dụng dữ kiện này như thế nào vào bài tập. Nếu ko có dữ kiện này,mình vẫn có thể giải được bình thường.Nhờ ad xem giúp nhé,tks ad.
Đúng rồi bạn ạ. Đề đó cho thừa dữ kiện. Theo mình là thế. 😀 Chính vì vậy nên dạng bài tập này ở các đề thi về sau không thấy cho dữ kiện kiểu này nữa. 🙂
Add ơi, ở phần Hệ số biến thiên CV = độ lệch chuẩn / tỷ suất lời kỳ vọng. Mà add ghi bị nhầm là ngược lại ạ.
Linh ơi, đúng là Ad bị nhầm. Ad sửa lại rồi. Cảm ơn bạn nhé. Bài đăng bao lâu mà chả ai báo cho là bị nhầm để sửa. 😀
cho em hỏi, cái tỉ suất sinh lợi của danh mục là các r(A), r(B), r(C) là mình dùng r trung bình hay là lấy r của mỗi ngày ạ? Vì cái bảng của em nó cho r mỗi ngày chứ không có cho sẵn R của từng cổ phiếu là bn cả ạ.
Hi Phương,
Ad chưa rõ ý em. Ý em là tỷ suất sinh lời của danh mục hay tỷ suất sinh lời của từng cổ phiếu? Là tỷ suất sinh lời kỳ vọng hay chỉ là tỷ suất sinh lời?
Tỷ suất sinh lời bản chất nó là tỷ lệ giữa lợi nhuận thu được cho 1 giai đoạn đầu tư / vốn đầu tư ban đầu. Do vậy nó sẽ gắn với giai đoạn/thời kỳ chứ Ad không nghĩ là nó gắn theo ngày.
Còn tỷ suất sinh lời kỳ vọng của 1 cổ phiếu thì nó là tỷ suất sinh lời trung bình của cổ phiếu đó tại các điều kiện thị trường khác nhau. Và vì cũng là tỷ suất sinh lời nên nó cũng gắn với giai đoạn.
add ơi ! trong đề lẻ năm 2020 có ra dữ kiện là muốn xây dựng 1 danh mục Q gồm 2 CP trên sao cho Beta của danh mục này = Beta của danh mục thị trường thì phải kết hợp đầu tư 2 CP với Tỷ trọng bao nhiêu ? Mình chưa hiểu là phải tính Beta của danh mục thị trường như thế nào ?
Hi bạn, beta là hệ số phản ánh mức độ biến động lợi nhuận của 1 tài sản với thị trường. Do vậy, danh mục thị trường thì sẽ luôn có beta = 1 => Mục tiêu là xây dựng tỷ trọng danh mục để có βp = 1